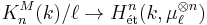Norm residue isomorphism theorem

In the mathematical field of algebraic K-theory, the norm residue isomorphism theorem is a long-sought result whose complete proof was announced in 2009. It previously was known as the Bloch–Kato conjecture, after Spencer Bloch and Kazuya Kato, or more precisely the motivic Bloch–Kato conjecture in some places, since there is another Bloch–Kato conjecture on values of L-functions.

It is a generalisation of the Milnor conjecture of K-theory, which was proved in the 1990s by Vladimir Voevodsky, the Milnor conjecture being the 2-torsion part of the Bloch–Kato conjecture. The point of the conjecture is to equate the torsion in a K-group of a field F, algebraic information that is in general relatively inaccessible, with the torsion in a Galois cohomology group for F, which is in many cases much easier to compute. Now that the complete proof of the Bloch–Kato conjecture has been announced, due to several mathematicians and contained in quite a number of papers, the result is also known as the Voevodsky–Rost theorem, for Voevodsky and Markus Rost. The title "norm residue" uses the analogy with standard local class field theory to identify the result conjectured and now announced in terms of its function in a "higher" class field theory, still being developed.

The norm residue isomorphism theorem implies the Quillen–Lichtenbaum conjecture.

Statement

The norm residue isomorphism theorem (or Bloch-Kato conjecture) states that for a field k and an odd prime l that is invertible in k, the norm residue map

K_n^M(k)/\ell \to H^n_{{\acute{\rm e}{\rm t}}}(k,\mu^{\otimes n}_\ell)

from Milnor K-theory mod l to étale cohomology is an isomorphism. The corresponding statement for l=2 is the Milnor conjecture that was proved earlier by Voevodsky.

References